Find the Ratio of the Masses M1 M2

Up to 256 cash back If they have the same non-zero linear momentum find the ratio of their kinetic Get the detailed answer. Using the fact that you say the velocities can be interchanged we obtain a final answer of.

Two Bodies Of Masses M 1 And M 2 Have Same Kinetic Energy The Ratio Of Their Momentum Is Youtube

W sqrt km w2 km w1w229 m1m2m1 9 1 m2m1 check my thinking.

. M 1 u 1 v 1 m 2 v 2 u 2 Allowing us to rearrange to. The ratio of distance of the particles of masses m1 and m2 from their centre of mass is. K is the spring constant.

The blocks are displaced by 10 cm then released. K m2 Σ h m m1m2 923 PM arch LO Th 72F 3242022 Home End Insert Delete F10 F11 F12 Backspac 5 7 8 9. M1m2 15 oz 15 oz 15 oz Which massis closer.

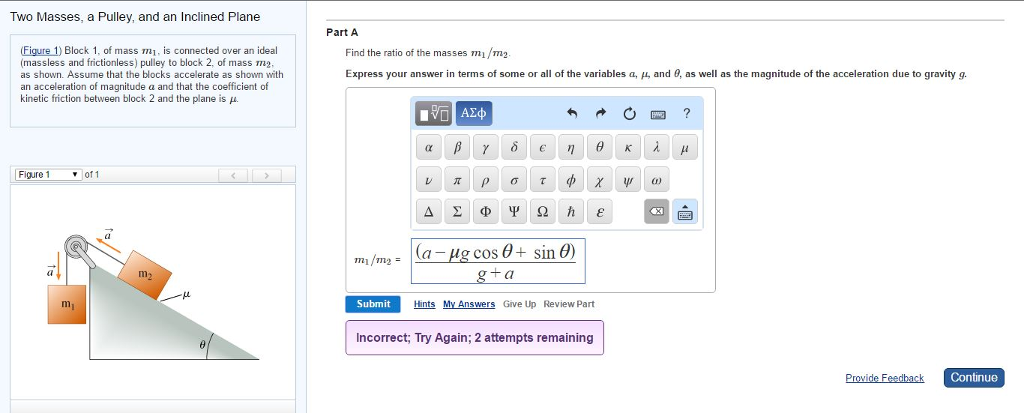
Find the ratio m2m1 of the masses. Express your answer in terms of some or all of the variables a μ and θ as well as the magnitude of the acceleration due to gravity g. That means its moving along the right direction.

A second mass m 2 accelerates at 10 ms 2 when F is applied to it. Kg - g sinθ - μ g cos θ K 1 a Ka a. Now you can substitute the formula of.

Find the value of the ratio m 1 m 2. When an object of mass m1 is hung on a vertical spring and set into vertical simple harmonic motion its frequency is 12 Hz. Express your answer in terms of some or all of the variables a μ and Πas well as the magnitude of the acceleration due to gravity g.

The masses of the blocks are. Express your answer in terms of some or all of the variables a and as well as the magnitude of the acceleration due to gravity g. When another object of mass m2 is hung on the spring along with m1 the frequency of the motion is 4 Hz.

D1d2 1 3 Larger Massm1 15 15 15 Smaller Mass m2 1 1 1 Ratio. A mass m 1 accelerates at 3 ms 2 when a force F is applied. The momentum of the center of mass is given by Mv m₁v₁ m₂v₂ where.

The ratio m_2m_1 of the masses is 9745. Find the ratio of the masses m1m2. A A point-like mass m1 travelling with speed v1 collides elastically head-on with a particle of mass m2 initially at rest.

Find the ratio of the masses m1m2. And on the other hand for another mass M2 the velocity is observed to be -74 ms. Two stones A and B are dropped from the top of two different towers such that they travel 4 4.

7 m in the last second of their motion respectively. Write equations for the conserved quantities before and after the collision and derive an expression for the speed v2 of mass m2 after the collision as a function of the masses and the impact velocity v1 only. Find the acceleration of the combined mass m 1 m 2 under the action of the force F.

1 m 1 m 2 and the energy in ratio 1. M1g - m2g sinθ - μ m2g cos θ m1 m2 a. A block with mass M 500 kg rests on a frictionless table and is attached by a horizontal spring k 130 Nm to a wall.

Formula for frequency when mass m_2 is hung on the spring along with m_1. So particle one It has mass M1 and it moves with a velocity of three point two ms. M 1 m 2 v 2 v 1 v 2 v 1.

Find the ratio of the heights of the two towers from where the stones were dropped. View Available Hints Figure K 1 of 1. M1g - m2g sinθ - μ m2g cos θ and this pulls the two masses.

1 m and 6 3. M 1 m 2 v 2 u 2 u 1 v 1. You have two masses m1 and m2 where m2 917m1.

Now the two bodies lets say m 1 and m 2 have ratio of masses as 3. Formula for frequency when mass m_1 is hung on the spring. M1 810kg and M2 390kg.

On Solving the above equation. So for mass one the velocities plus three point two ms. In order to find ratio m_2m_1 Divide the above equations.

M1 and m2 with an acceleration a. Dividing by m2 and expressing m1m2 as K. Calculate the tension in the.

K g- a a g sinθ μ cosθ m1m2 a g sinθ μ cosθ g- a. Ratio m₁m₂ of mass of particles. FILL IN THE TABLE BELOW WITH YOUR RESPONSES FOR THE THREE DIFFERENT CASES Case 1 Case 2 Case 3 LongerDistance d1 8 135 1575 ShorterDistance d2 8 45 225 Ratio.

Express your answer in terms of some or all of the variables a u and 0 as well as the magnitude of the free-fall acceleration g. Find the ratio of the masses m1m2. 7 M2 M2 M2.

This final step gives a ratio of 1. But here we just divide 74 with 32 To get the ratio as two. K is the spring constant.

M combined mass of particles m₁ m₂ v velocity of center of mass 0 ms m₁ mass of particle 1 v₁ velocity of particle 1 32 ms m₂ mass of particle ₂ v₂ velocity of particle 2 -71 ms. You have two masses m1 and m2 where m2 917m1. Find the ratio of the masses m1m2.

A second block of mass m 125 kg rests on top of M.

Solved Figure 1 Block 1 Of Mass M 1 Is Connected Over An Chegg Com

Solved Part A Figure 1 Block 1 Of Mass M1 Is Connected Chegg Com

Ratio Of Two Masses Connected By Pulley Physics Forums

Two Bodies Have Their Masses As M1 M2 With A Ratio Of 3 1 If Their Kinetic Energies Have A Ratio Such As E1 E2 As 1 3 How Do You Find The Ratio Of Their